Chapter 4: Graphs

Graphs
19:14

Definition (Graph)

An undirected graph is a set $G = V \times E$ where

E \subset {{v, w} : v, w \in V}

Remarks

The elements of V are called vertices
The elements of E are called edges
If instead $E \subset {(v, w) : v, w \in V}$ , the graph is called directed

Adjacency matrix
19:14

Definition (Adjacency matrix)

Assume $V = {1, \dots, n}$

a_{ij} = {10 if there’s an edge from i t o j otherwise

Random browsing
19:14

Each page has the same probability of being the start page
There is at most one link from one page to any other
On each page, each link has the same probability of being clicked
If there are no links, the next page can be any page with equal probability

Ranking webpages
19:14

$X_{k}$ : k-th page visited
$P (X_{k} = i)$ : probability that the k-th page is page $i$

Idea

If $k$ is small, $P (X_{k} = i)$ depends too much on $X_{0}$ . A good way to measure the popularity of page $i$ would be

p_{i} = def k \to + \infty lim P (X_{k} = i)

Rank and PageRank
19:14

p^{(k)} = def P (X_{k} = 1) P (X_{k} = 2) ⋮ P (X_{k} = n - 1) P (X_{k} = n)

Definition (PageRank vector)

p^{(\infty)} = k \to + \infty lim p^{(k)}

Transition Matrix
19:14

T_{ij} = def P (X_{k + 1} = i ∣ X_{k} = j)

Properties of the transition matrix
19:14

Proposition

p^{(k + 1)} = T p^{(k)}

Corollary

The PageRank vector satisfies

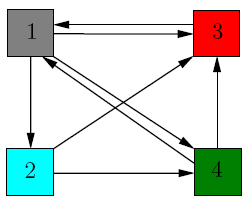
p^{(\infty)} = T p^{(\infty)}

Weakness of naive PageRank
19:14

Question

What's the issue with the above graphs? How would you fix it?

PageRank algorithm
19:14

Idea

Approximate $p^{(\infty)} \approx p^{(k)}$ for some large $k$ via

p^{(k + 1)} = T p^{(k)}

Exercise

Implement it on this dataset

Show the ten highest ranked pages.

PageRank: solution
19:14

Graph Exploration
19:14

Question

From a given set of nodes, which vertices can I reach?

Web crawling
Social networking
Network Broadcast
Garbage collection

Adjacency list
19:14

Definition (Adjacency list)

Adj [u] = {v \in V ∣ (u, v) \in E}

Question

How much space does that representation required?

$Θ (V + E)$

Adjacency list/matrix
19:14

Breadth-first search
19:14

Visit all the nodes reachable from a given node $s \in V$
We want to achieve $O (V + E)$ time
Look at nodes reachable in $0, 1, 2, \dots$ moves
Careful to avoid duplicates (otherwise running time could be infinite)

Breadth-First Search
19:14

Exercise

Write an algorithm that perform breadth-first search from a given source node s.

Shortest paths
19:14

Exercise (Shortest paths)

Change the BFS algorithm so that you can keep track of a shortest path from s to any node.

Running Time
19:14

Proposition

v \in V \sum ∣ Adj [v] ∣ = Θ (E)

Depth-first search
19:14

Recursively explore graph, backtracking as necessary
Careful not to repeat

Exercise

Implement DFS, when you're given the set of vertices and an adjacency list.

DFS: Running time
19:14

Proposition

The Running time of DFS is $Θ (V + E)$

Exercise: Sudoku solving
19:14

Exercise (Sudoku Solving)

Sudoku is a puzzle where you're given a 9 by 9 grid partially filled with digits. The objective is to fill the grid subject to the constraint that every row, column, and box (3 by 3 subgrid) must contain all of the digits from 1 to 9.

Exercise: N queens problem
19:14

Recall: DFS
19:14

Recursively explore graph, backtracking as necessary
Careful not to repeat

Sudoku: solution
19:14

Edge classification
19:14

Tree edge: visit new vertex via edge
Forward edge: node to descendant in a tree but not a tree edge
Backward edge: node to ancestor in tree, indicate a cycle
Cross edge: between two non-ancestor related vertices

Question

How can we know what type of edge $(u, v)$ is?

Tree edges: $v$ is white when we explore edge
Forward edge: $v$ is black when we explore edge
Back edge: $v$ is gray when we explore edge
Cross edge: $v$ is black when we explore edge

Edge classification in undirected graphs
19:14

Proposition

In an undirected graph, every edge is either a tree or a backedge.

Corollary

An undirected graph is acyclic if and only if there are no back edges

Acyclic directed graphs
19:14

Proposition

A directed graph is acyclic if and only if there are no back edges.

Topological Sort
19:14

Problem

Given a directed acyclic graph, "sort" the vertices in such a way that the edges are always pointing to the right.

Applications include:

Building software
Job scheduling
Select courses with prerequisites

Topological sort: example
19:14

Topological sort: algorithm and proof of correctness
19:14

Run DFS
Output vertices in decreasing order of finish time

Proposition

If $(u, v) \in E$ , then

u . f \geq v . f

Topological sort: implementation
19:14

Exercise

Modify DFS to implement topological sort

Exercices
19:14

Strongly Connected Component
19:14

Definition (Strongly connected component)

Let $G = (V, E)$ be a directed graph. A subset $C \subset V$ is a strongly connected component if for every pair $u, v \in C$ , there is a path from $u$ to $v$ and from $v$ to $u$ .

Definition (Component graph)

Let $G = (V, E)$ be a directed graph with connected connected $C_{1}, \dots, C_{n}$ . The component graph is the graph

{C_{i} : 1 \leq i \leq n} \times {(C_{i}, C_{j}) : 1 \leq i, j \leq n and there’s a path between C_{i} and C_{j}}

Strongly connected components
19:14

Problem

Given a directed graph G, find its connected components

Remark

DFS-Visit will always visit at least the connected component of the starting point, but might visit other connected components too.
Between two strongly connected components, there's a one-way bridge between them.

Transpose graph
19:14

Definition (Transpose graph)

Let $G = (V, E)$ be a graph. Its transpose graph is the graph

V \times {(v, u) : (u, v) \in E}

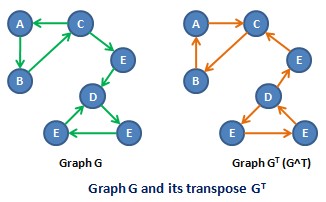
Question

Why is it called the transpose graph? What happens to the adjacency matrix when we transpose the graph?

Exercise

Write a Python code that transforms a graph (given via an adjacency list) to its transpose.

Strongly connected components: algorithm
19:14

Topological sort the edges of the graphs
Transpose the graph
Run DFS visit on unvisited nodes in the order given in Step I.

Exercise

Implement it

Strongly connected components: proof of correctness
19:14

Proposition

Assume that $S_{1}, \dots, S_{n}$ are the strongly connected components of a graph $G = (V, E)$ in the order given by the SCC algorithm.

If $s \in S_{i}$ , then DFS-Visit will only reach the vertices in $S_{1}, \dots, S_{i}$ in the transpose of $G$ .

Corollary

The SSC algorithm is correct.

Weighted graph
19:14

Definition

A graph $G = (V, E)$ is weighted if it's given with a function $w : E \to R$ .

Minimum spanning tree
19:14

Problem

Given an undirected weighted and connected graph $((V, E), w)$ , find a spanning subtree $T \subset E$ with smallest total weight.

Edge contraction
19:14

Definition (Edge contraction)

$G / e$ : Remove edge and merge the vertices it previously joined

Question

What did we do about common neighbours?

Dynamic programming solution
19:14

Guess edge $e$ in a MST
Contract $e$
Recurse
Decontract $e$ and add $e$ to MST

Remark (Greedy)

We will remove the guessing part by proving that the greedy choice is optimal

Question

What's the time complexity?

Correctness of the DP algorithm
19:14

Proposition

Assume $e$ belongs to some MST $T^{*}$ of $G$ . If $T^{'}$ is a MST of $G / e$ , then $T^{'} \cup {e}$ is a MST of G

Sketch proof

w (T^{'} \cup {e}) = w (T^{'}) + w (e) \leq w (T^{*} ∖ {e}) + w (e) = w (T^{*})

Definitions
19:14

Cut: partition of the vertices in two sets $(S, V ∖ S)$
Edge $(u, v)$ crosses cut $S$ if $u \in S, v \in V ∖ S$ or vice-versa.
Cut respects $A$ if no edge in $A$ crosses the cut.
light edge crossing a cut: minimal weight of any edge entering the cut.

Criterion for safe edge
19:14

The greedy choice works.

Proposition

Assume $A \subset E$ is a subset of some MST.

If $S$ is a cut respecting $A$ and $(u, v)$ is a light edge crossing $(S, V ∖ S)$ , then $(u, v)$ is also part of some MST.

We've reduced guessing an edge to using a particular cut respecting $A$ .

Greedy Generic MST algorithm
19:14

A = {}
while A is not spanning:
    find safe edge e
    A.add(e)
return A

We'll see: Prims, Kruskal

Prim's Algorithm: Idea
19:14

Start at vertex $s$
Cut will be the visited vertices
Maintain a priority queue containing crossing edges. Prioritize lighter edges.

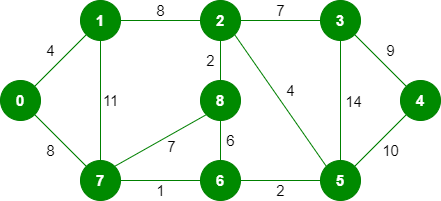
Example

Find the MST of the following graph

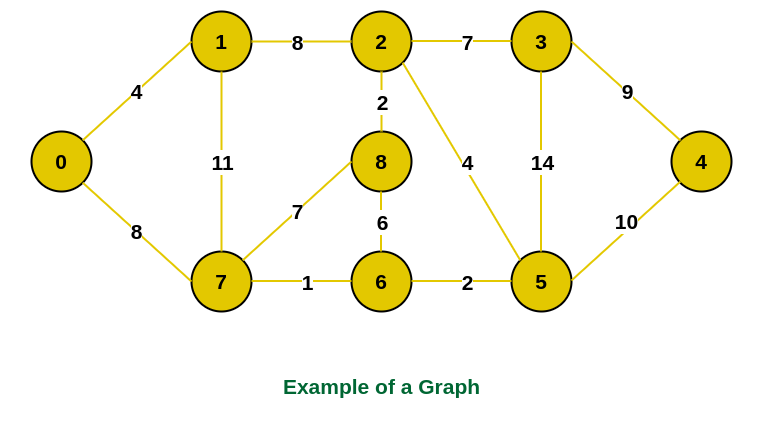
Prim's Algorithm: Python implementation
19:14

Question

How would we get the tree itself?

Prim: Time complexity
19:14

Proposition

The time complexity of this algorithm is $O ((V + E) lo g V)$

V \times O (1) + pop O (V lo g V) + push O (E lo g V)

Kruskal's algorithm
19:14

Union-Find structure
19:14

Idea

Keep track of connected components

We'll need two operations to apply Kruskal

Union: unites two components
Find: finds an element's component

Union-Find structure: Python implementation
19:14

Kruskal's implementation
19:14

Graphs19:14

Definition (Graph)

Remarks

Adjacency matrix19:14

Definition (Adjacency matrix)

Random browsing19:14

Ranking webpages19:14

Idea

Rank and PageRank19:14

Definition (PageRank vector)

Transition Matrix19:14

Properties of the transition matrix19:14

Proposition

Corollary

Weakness of naive PageRank19:14

Question

PageRank algorithm19:14

Idea

Exercise

PageRank: solution19:14

Graph Exploration19:14

Question

Adjacency list19:14

Definition (Adjacency list)

Question

Adjacency list/matrix19:14

Breadth-first search19:14

Breadth-First Search19:14

Exercise

Shortest paths19:14

Exercise (Shortest paths)

Running Time19:14

Proposition

Depth-first search19:14

Exercise

DFS: Running time19:14

Proposition

Exercise: Sudoku solving19:14

Exercise (Sudoku Solving)

Exercise: N queens problem19:14

Recall: DFS19:14

Sudoku: solution19:14

Edge classification19:14

Question

Edge classification in undirected graphs19:14

Proposition

Corollary

Acyclic directed graphs19:14

Proposition

Topological Sort19:14

Problem

Topological sort: example19:14

Topological sort: algorithm and proof of correctness19:14

Proposition

Topological sort: implementation19:14

Exercise

Exercices19:14

Strongly Connected Component19:14

Definition (Strongly connected component)

Definition (Component graph)

Strongly connected components19:14

Problem

Remark

Transpose graph19:14

Definition (Transpose graph)

Question

Exercise

Strongly connected components: algorithm19:14

Exercise

Strongly connected components: proof of correctness19:14

Proposition

Corollary

Weighted graph19:14

Definition

Minimum spanning tree19:14

Problem

Edge contraction19:14

Definition (Edge contraction)

Question

Dynamic programming solution19:14

Graphs
19:14

Adjacency matrix
19:14

Random browsing
19:14

Ranking webpages
19:14

Rank and PageRank
19:14

Transition Matrix
19:14

Properties of the transition matrix
19:14

Weakness of naive PageRank
19:14

PageRank algorithm
19:14

PageRank: solution
19:14

Graph Exploration
19:14

Adjacency list
19:14

Adjacency list/matrix
19:14

Breadth-first search
19:14

Breadth-First Search
19:14

Shortest paths
19:14

Running Time
19:14

Depth-first search
19:14

DFS: Running time
19:14

Exercise: Sudoku solving
19:14

Exercise: N queens problem
19:14

Recall: DFS
19:14

Sudoku: solution
19:14

Edge classification
19:14

Edge classification in undirected graphs
19:14

Acyclic directed graphs
19:14

Topological Sort
19:14

Topological sort: example
19:14

Topological sort: algorithm and proof of correctness
19:14

Topological sort: implementation
19:14

Exercices
19:14

Strongly Connected Component
19:14

Strongly connected components
19:14

Transpose graph
19:14

Strongly connected components: algorithm
19:14

Strongly connected components: proof of correctness
19:14

Weighted graph
19:14

Minimum spanning tree
19:14

Edge contraction
19:14

Dynamic programming solution
19:14

Correctness of the DP algorithm
19:14

Definitions
19:14

Criterion for safe edge
19:14

Greedy Generic MST algorithm
19:14

Prim's Algorithm: Idea
19:14

Prim's Algorithm: Python implementation
19:14

Prim: Time complexity
19:14

Kruskal's algorithm
19:14

Union-Find structure
19:14

Union-Find structure: Python implementation
19:14

Kruskal's implementation
19:14

Kruskal: correctness
19:14