Chapter 5: Graphs (part II)

Single-Source Shortest paths
18:16

Problem

Given a directed graph with nonnegative weights on the edges and a source vertex $s \in V$ , find a shortest path from $s$ to any $v \in V$ .

Remark

We might only care about one pair of vertices, but these problems have the same time complexity.
If the weights are all one, this was solved by $BFS$ .
Later: negative weights with Bellman-Ford.

Animation
18:16

Dijkstra's algorithm: idea
18:16

Start at $s$
Keep a heap with a good guess of the distance
Go to the next vertex in the queue
Update distances for the neighbours of that vertex

Dijkstra's algorithm
18:16

Dijkstra: correctness and complexity
18:16

δ (s, v) = def s ⇝ v min e \in edge (s ⇝ v) \sum w (e)

Proposition (Dijkstra: correctness)

After a vertex $v$ leaves the queue,

distances [v] = δ (s, v)

Sketch proof

Assume we're about to add $u$
Shortest path: $s ⇝ x \to y ⇝ u$

distances [u] \leq distances [y] \leq δ (s, y) \leq δ (s, u)

Proposition

The time complexity is $O ((V + E) lo g V)$

A*
18:16

Exercise

Implement the $A^{⋆}$ algorithm, which brings the following changes to Dijkstra:

Stop as soon as we've reached our goal
Instead of pushing the distance to the heap, use $dist (v) + heuristic (v)$

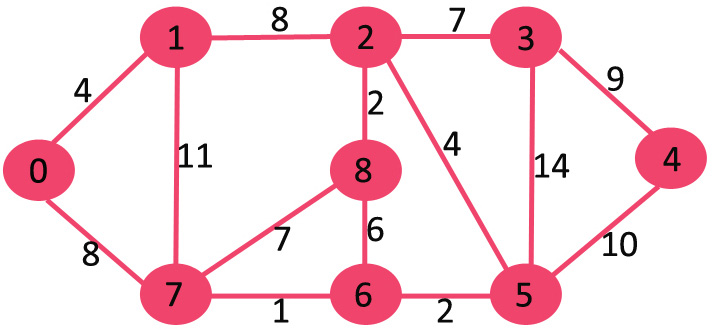
Apply A* to the graph below:

Exercises: A*
18:16

Exercise

How would you find the actual shortest path?

Define a heuristic to avoid a particular airport

Exercise

Why doesn't the algorithm work for negative weights?

Exercises
18:16

Dijkstra: recap
18:16

Bellman-Ford
18:16

Dijkstra is an efficient algorithm if the weights associated with the edges are nonnegative.

Example

Apply Dijkstra to this graph (we'll apply Bellman-Ford afterwards) with $A$ as a starting point

Bellman-Ford: implementation
18:16

Exercise

Implement Bellman-Ford to find the length of the shortest path. What's its time complexity?

Exercise

How would you get the actual path as well?

Bellman-Ford: correctness
18:16

Theorem (Correctness of Bellman-Ford)

Assume $G$ has no negative-weight cycles that are reachable from $s$ .

At the end of the algorithm,

d [v] = δ (s, v) .

for all vertices $v$ that are reachable from $s$ .

Sketch proof

Let $s v_{0}, v_{1}, \dots, v_{k - 1}, v v_{k}$ be a shortest path.
$k \leq ∣ V ∣ - 1$
Loop invariant: at the beginning of each iteration $d [v_{0}] = δ (s, v_{0}) d [v_{1}] = δ (s, v_{1}) \dots d [v_{i}] = δ (s, v_{i})$

Detecting negative-weight cycles
18:16

Proposition

A graph contains a negative cycle reachable from $s$ if and only if one edge can be relaxed at the end of Bellman-Ford.

Sketch proof

$\Leftarrow$ : previous correctness result
$\Rightarrow$ : $i = 1 \sum k d [v_{i}] \leq i = 1 \sum k (d [v_{i - 1}] + w (v_{i - 1}, v_{i}))$

Detecting negative-weight cycles: implementation
18:16

Exercise

Change your Bellman-Ford code so that it detects negative cycle reachable from the source

Exercises
18:16

All Pairs Shortest Paths
18:16

Problem

Find the shortest path between all pairs of vertices

Question

What would the time complexities be if we applied Bellman-Ford or Dijkstra and iterate through all vertices for the source node?

We'll try to use dynamic programming to get a better time complexity.

1st attempt: guess next-to-last vertex
18:16

Subproblem: DP(u, v, k): length of shortest path $u ⇝ v$ using at most $k$ edges
Guess: Next-to-last vertex
Base cases: $DP (u, v, 0) = {0 + \infty if u = v$
Recurrence: $DP (u, v, k) = min {DP (u, v, k - 1), y \in V min [D P (u, y, k - 1) + w (y, v)]}$

Python implementation of the first attempt
18:16

Exercise

What is the time complexity?

Combining DP and D&C
18:16

Question

What if we guess the middle vertex instead of the penultimate? What would the time complexity be?

Floyd-Warshall
18:16

Before, APSP(u, v, k) added the constraint that the SP used at most $k$ edges. The guessing part is $O (V)$ .

Idea

FW(u, v, k): minimum weight of a path via first $k$ vertices.

Subproblem: FW(u, v, k): minimum weight of path via first $k$ vertices
Guess: Should we include the $(k + 1)$ th vertex?
Base cases: $FW (u, u, k) =$ $FW (u, v, 0) = {$
Recursion: $FW (u, v, k) =$
Time complexity

Python implementation of Floyd-Warshall
18:16

Single-Source Shortest paths18:16

Problem

Remark

Animation18:16

Dijkstra's algorithm: idea18:16

Dijkstra's algorithm18:16

Dijkstra: correctness and complexity18:16

Proposition (Dijkstra: correctness)

Proposition

A*18:16

Exercise

Exercises: A*18:16

Exercise

Exercise

Exercises18:16

Dijkstra: recap18:16

Bellman-Ford18:16

Example

Bellman-Ford: implementation18:16

Exercise

Exercise

Bellman-Ford: correctness18:16

Theorem (Correctness of Bellman-Ford)

Sketch proof

Detecting negative-weight cycles18:16

Proposition

Sketch proof

Detecting negative-weight cycles: implementation18:16

Exercise

Exercises18:16

All Pairs Shortest Paths18:16

Problem

Question

1st attempt: guess next-to-last vertex18:16

Python implementation of the first attempt18:16

Exercise

Combining DP and D&C18:16

Question

Floyd-Warshall18:16

Idea

Python implementation of Floyd-Warshall18:16

Single-Source Shortest paths
18:16

Animation
18:16

Dijkstra's algorithm: idea
18:16

Dijkstra's algorithm
18:16

Dijkstra: correctness and complexity
18:16

A*
18:16

Exercises: A*
18:16

Exercises
18:16

Dijkstra: recap
18:16

Bellman-Ford
18:16

Bellman-Ford: implementation
18:16

Bellman-Ford: correctness
18:16

Detecting negative-weight cycles
18:16

Detecting negative-weight cycles: implementation
18:16

Exercises
18:16

All Pairs Shortest Paths
18:16

1st attempt: guess next-to-last vertex
18:16

Python implementation of the first attempt
18:16

Combining DP and D&C
18:16

Floyd-Warshall
18:16

Python implementation of Floyd-Warshall
18:16