Champs de vecteurs - partie II

Chapitre 3

Résumé de l'intégration sur les courbes et surfaces
04:23

	Courbes planaires	Surfaces
Paramétrisation	$r (t)$	$r (u, v)$
Plan tangent	$\frac{d r}{d t}$ : vecteur directeur	$\frac{\partial r}{\partial u}, \frac{\partial r}{\partial v}$ : vecteurs directeurs $\frac{\partial r}{\partial u} \times \frac{\partial r}{\partial v}$ : vecteur normal
Élément de longueur/surface	$d s = \frac{d r}{d t} d t$	$d S = \frac{\partial r}{\partial u} \times \frac{\partial r}{\partial v} d A$
Élément de longueur/surface (graphe)	$d s = 1 + (\frac{d y}{d x})^{2} d x$	$d S = 1 + (\frac{\partial z}{\partial x})^{2} + (\frac{\partial z}{\partial y})^{2} d x d y$
Intégration de champs de vecteurs	$d r = \frac{d r}{d t} d t$ (circulation)	$d S = \frac{\partial r}{\partial u} \times \frac{\partial r}{\partial v} d A$ (flux)

Paramétrisation de surfaces et élément d'aire
04:23

Si une surface $S$ est paramétrée par

r (u, v) = x (u, v) i + y (u, v) j + z (u, v) k, (u, v) \in D

alors

d S = ∥ \partial_{u} r \times \partial_{v} r ∥ d u d v

Exemple: aire de la sphère
04:23

Example

Trouvez la surface d'une sphère de rayon $a$ .

Recall (Coordonnées sphériques)

x y z = a sin ϕ cos θ = a sin ϕ sin θ = a cos ϕ

Paramétrisation de graphes
04:23

Si la surface $S$ est un graphe, alors une paramétrisation est donnée par

r (x, y) = x i + y j + z (x, y) k .

On vérifie par calculs que

d S = ∥ \partial_{u} r \times \partial_{v} r ∥ d u d v = 1 + (\frac{\partial z}{\partial x})^{2} + (\frac{\partial z}{\partial y})^{2} d x d y

Il est utile de pouvoir utiliser cette formule directement plutôt que de la recalculer.

Aire d'un graphe
04:23

Recall

d S = 1 + (\frac{\partial z}{\partial x})^{2} + (\frac{\partial z}{\partial y})^{2} d x d y

Example

Trouvez l'aire de la partie du paraboloïde $z = x^{2} + y^{2}$ qui se trouve sous le plan $z = 9$

Intégration sur une surface
04:23

Example

\iint_{S} x^{2} d S, S : sph \overset{e}{ˋ} re unit \overset{e}{ˊ}

Recall

x y z = r sin ϕ cos θ = r sin ϕ sin θ = r cos ϕ

d S r = ∥ \partial_{u} r \times \partial_{v} r ∥ d u d v = 1

Intégration sur un graphe
04:23

Example

\iint_{S} y d S

où $S$ est la surface

z = x + y^{2}, 0 \leq x \leq 1, 0 \leq y \leq 2

Recall

d S = 1 + (\frac{\partial z}{\partial x})^{2} + (\frac{\partial z}{\partial y})^{2} d x d y

Surfaces orientées
04:23

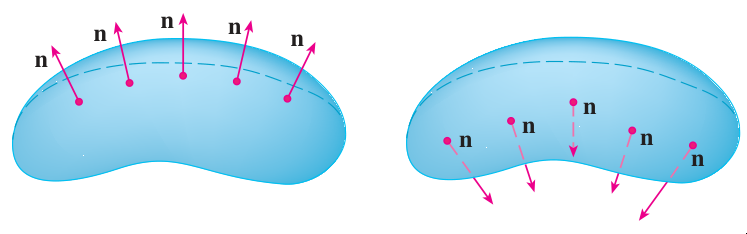
L'intégrale de champ de vecteurs ne peut se faire que sur une surface orientée.

Definition (Orientation)

Une orientation est la donnée d'un champ continu de vecteurs normaux unitaire

Orientation d'un graphe
04:23

Recall

N = \partial_{u} r \times \partial_{v} r

Pour un graphe $z = f (x, y)$ nous avons

N = - \frac{\partial f}{\partial x} i - \frac{\partial f}{\partial y} j + k

Flux
04:23

Definition (Flux)

\iint_{S} F \cdot d S n d S

\iint_{S} F \cdot d S = \iint_{D} F \cdot (\frac{\partial r}{\partial u} \times \frac{\partial r}{\partial v}) d A

En particulier, pour un graphe:

\iint_{S} F \cdot d S = \iint_{D} F \cdot (- \frac{\partial z}{\partial x} i - \frac{\partial z}{\partial y} j + k) d x d y

Flux: exemple
04:23

Example

Calculez le flux de $F (x, y, z) = z i + y j + x k$ à travers la sphère unité

Recall

\iint_{S} F \cdot d S = \iint_{D} F \cdot (\frac{\partial r}{\partial u} \times \frac{\partial r}{\partial v}) d A

Flux à travers un graphe
04:23

Recall

d S = - \frac{\partial z}{\partial x} i - \frac{\partial z}{\partial y} j + k

Example

\iint_{S} F \cdot d S, F (x, y, z) = def y i + x j + z k,

$S$ entre $z = 1 - x^{2} - y^{2}$ et $z = 0$

Orientation induite sur le contour
04:23

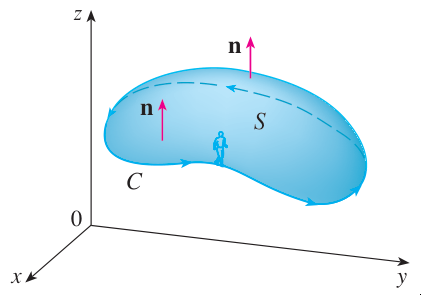
Théorème de Stokes
04:23

Theorem

Si $S$ est gentille et orientée et sa frontière $C$ est aussi gentille avec l'orientation induite,

\int_{C} F \cdot d r = \iint_{S} \nabla \times F \cdot d S

Si $S$ est un rectangle, c'est le théorème de Green.

Si $S_{1}, S_{2}$ sont deux surfaces avec le même contour, alors

\iint_{S_{1}} \nabla \times F \cdot d S = \iint_{S_{2}} \nabla \times F \cdot d S

Stokes: exemple
04:23

Example

\int_{C} F \cdot d r, F (x, y, z) = - y^{2} i + x j + z^{2} k,

où $C$ est l'intersection entre le plan $y + z = 2$ et le cylindre $x^{2} + y^{2} = 1$ , orienté dans le sens anti-horloger vu par le dessus.

Stokes: exemple
04:23

Example

\iint_{S} \nabla \times F \cdot d S, F (x, y, z) = x z i + yz j + x y k

où $S$ est la partie de la sphère $x^{2} + y^{2} + z^{2} = 4$ contenue dans le cylindre $x^{2} + y^{2} = 1$ et au-dessus du plan $x y$ .

Interprétation du rotationnel
04:23

masse charge circulation = \iint_{S} densit \overset{e}{ˊ} de masse ρ (x, y, z) d S = \iint_{S} densit \overset{e}{ˊ} de charge σ (x, y, z) d S = \iint_{S} ? \nabla \times F \cdot n d S

Remark

Le rotationnel représente la densité de circulation

Théorème de la divergence
04:23

Theorem (Divergence (Ostrogradsky))

Soit une région simple $E$ dont la surface $S$ est munie de l'orientation extérieure.

\iint_{S} F \cdot d S = ∭_{E} \nabla \cdot F d V

Preuve lorsque $E = [a_{1}, b_{1}] \times [a_{2}, b_{2}] \times [a_{3}, b_{3}]$

Remark

Le théorème de la divergence généralise le théorème fondamental de l'analyse

\int_{a}^{b} f^{'} (x) d x = f (b) - f (a)

Exemple: calcul de flux
04:23

Exercise

Trouvez le flux du champ $F (x, y, z) = z i + y j + x k$ à travers la sphère unité.

Exemple: calcul de flux
04:23

Example

F (x, y, z) = x y i + (y^{2} + e^{x z^{2}}) j + sin (x y) k

où

S

est la surface de la région

E

délimitée par

z = 1 - x^{2}

z = 0

y = 0

y + z = 2

Théorème de Gauss
04:23

Theorem

Soit le champ donné par

E = \frac{1}{4 π ε _{0}} \frac{Q}{∥ x ∥ ^{3}} x

Montrez que le flux ne dépend pas du choix de surface $S$ contenant l'origine et que

\iint_{S} E \cdot d S = \frac{Q}{ε 0}

Remark

Ce théorème est également vrai pour le champ gravitationnel classique.

Interprétation de la divergence
04:23

masse charge flux = ∭_{V} densit \overset{e}{ˊ} de masse ρ (x, y, z) d V = ∭_{V} densit \overset{e}{ˊ} de charge σ (x, y, z) d V = ∭_{V} ? \nabla \cdot F (x, y, z) d V

Rotationnel du rotationnel
04:23

Proposition

\nabla \times (\nabla \times A) = \nabla (\nabla \cdot A) - \nabla^{2} A

Application: Maxwell dans le vide
04:23

Exercise

Voici les équations de Maxwell.

\nabla \cdot E = \frac{ρ}{ε _{0}}, \nabla \times E = - \frac{\partial B}{\partial t}, \nabla \cdot B = 0, \nabla \times B = μ_{0} J + μ_{0} ε_{0} \frac{\partial E}{\partial t},

En prenant le rotationnel des équations rotationnelles, montrez que dans le vide, $E$ et $B$ vérifient l'équations d'une onde se déplaçant à la vitesse de la lumière quel que soit le repère.

Infos utiles:

\frac{1}{v ^{2}} \frac{\partial ^{2} u}{\partial t ^{2}} - \nabla^{2} u = 0 \overset{ˊ}{E} quation d’onde

Résumé de l'intégration sur les courbes et surfaces04:23

Paramétrisation de surfaces et élément d'aire04:23

Exemple: aire de la sphère04:23

Example

Recall (Coordonnées sphériques)

Paramétrisation de graphes04:23

Aire d'un graphe04:23

Recall

Example

Intégration sur une surface04:23

Example

Recall

Intégration sur un graphe04:23

Example

Recall

Surfaces orientées04:23

Definition (Orientation)

Orientation d'un graphe04:23

Recall

Flux04:23

Definition (Flux)

Flux: exemple04:23

Example

Recall

Flux à travers un graphe04:23

Recall

Example

Orientation induite sur le contour04:23

Théorème de Stokes04:23

Theorem

Stokes: exemple04:23

Example

Stokes: exemple04:23

Example

Interprétation du rotationnel04:23

Remark

Théorème de la divergence04:23

Theorem (Divergence (Ostrogradsky))

Remark

Exemple: calcul de flux04:23

Exercise

Exemple: calcul de flux04:23

Example

Théorème de Gauss04:23

Theorem

Remark

Interprétation de la divergence04:23

Rotationnel du rotationnel04:23

Proposition

Application: Maxwell dans le vide04:23

Exercise

Résumé de l'intégration sur les courbes et surfaces
04:23

Paramétrisation de surfaces et élément d'aire
04:23

Exemple: aire de la sphère
04:23

Paramétrisation de graphes
04:23

Aire d'un graphe
04:23

Intégration sur une surface
04:23

Intégration sur un graphe
04:23

Surfaces orientées
04:23

Orientation d'un graphe
04:23

Flux
04:23

Flux: exemple
04:23

Flux à travers un graphe
04:23

Orientation induite sur le contour
04:23

Théorème de Stokes
04:23

Stokes: exemple
04:23

Stokes: exemple
04:23

Interprétation du rotationnel
04:23

Théorème de la divergence
04:23

Exemple: calcul de flux
04:23

Exemple: calcul de flux
04:23

Théorème de Gauss
04:23

Interprétation de la divergence
04:23

Rotationnel du rotationnel
04:23

Application: Maxwell dans le vide
04:23